여러 대의 차량을 이용하여 최적의 배송 계획을 수립하는 문제를 VRP(Vehicle Routing Problem)라고 합니다.
어떤 계획이 최적인가에 대한 다양한 기준이 있을 수 있지만, 가장 일반적으로 사용되는 최적화 기준 중 하나는 차량의 이동 거리를 최소화하는 것입니다.
그러나 VRP 문제는 단순히 이동 거리뿐만 아니라 시간 제약이 추가된 버전도 있습니다. 이를 VRPTW(Vehicle Routing Problem with Time Windows)라고 하며, 차량이 각 목적지에 도착해야 하는 시간 창(Time Window)이 존재하는 경우를 의미합니다. 이 문제에서는 각 차량이 정해진 시간 내에 지정된 장소에 도착해야 하므로, 시간 관리가 중요한 요소로 추가됩니다.
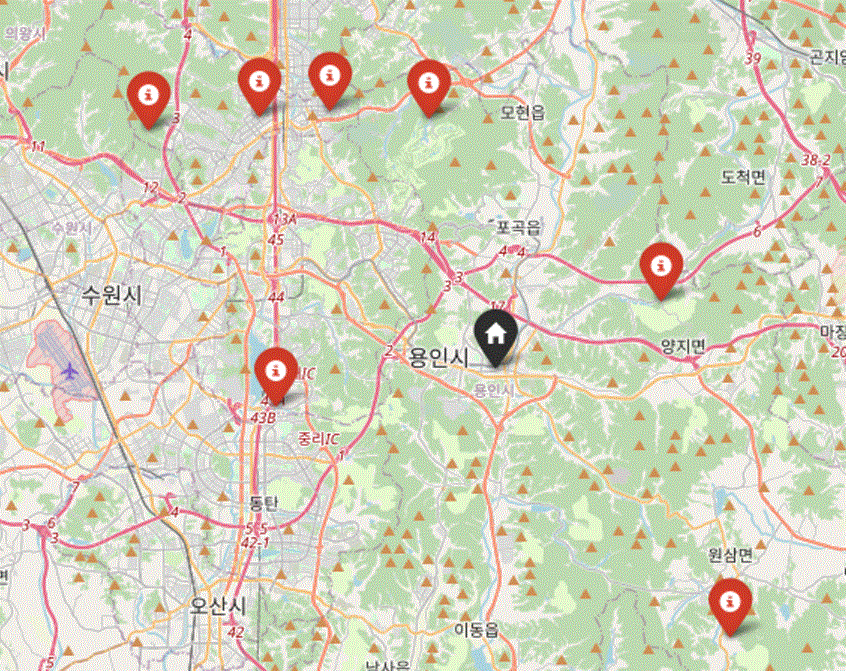
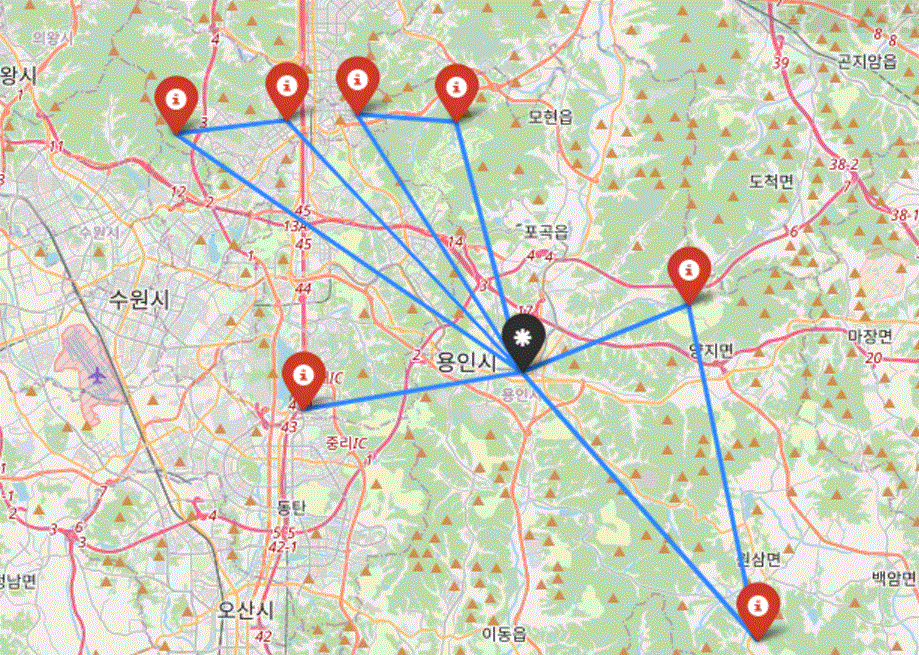
예를 들어, 아래 그림에서 검은색 아이콘으로 표시된 물류 창고에서 빨간색 아이콘으로 표시된 7개의 식당에 식재료를 조달해야 한다고 가정해보겠습니다. 이때 각 식당은 정해진 시간 창 내에만 식재료를 받을 수 있습니다. 오늘 사용할 수 있는 트럭은 총 4대이며, 모든 식당에 제시간에 배송을 완료하는 것이 목표입니다.
이 경우, 최소의 이동 거리뿐만 아니라 시간 제약을 준수하면서 각 트럭이 어느 순서로 어떤 식당에 배송해야 할지 결정하는 것이 VRPTW 문제에 해당합니다.
OR Tools에서는 VRP와 VRPTW 문제를 해결하기 위한 **특별한 라이브러리인 pywrapcp를 제공하며, 이를 활용하면 문제를 보다 쉽게 해결할 수 있습니다.
Routing 모델 생성
manager = pywrapcp.RoutingIndexManager(len(data['distance_matrix']), data['num_vehicles'], data['depot'])
routing = pywrapcp.RoutingModel(manager)
Python
복사
RoutingIndexManager 함수를 정의합니다. 이 함수는 3개의 인자를 받습니다.
•
첫 번째 인자: 거리 행렬(Distance Matrix)의 길이, 즉 고객(Customer)의 수.
•
두 번째 인자: 차량(Vehicle)의 수.
•
세 번째 인자: 창고 위치의 인덱스.
Distance Callback
def distance_callback(from_index, to_index):
from_node = manager.IndexToNode(from_index)
to_node = manager.IndexToNode(to_index)
return data['distance_matrix'][from_node][to_node]
transit_callback_index = routing.RegisterTransitCallback(distance_callback)
Python
복사
위 코드를 이용하면 Distance Matrix를 통해 두 노드 사이의 거리를 계산할 수 있습니다.
VRP 문제를 해결하기 위해 Distance Matrix를 사용할 수 있으며, routing.RegisterTransitCallback 함수를 이용해
이 거리를 비용으로 계산하도록 Distance Matrix를 routing 모델에 연동할 수 있습니다.
Travel Cost 세팅
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)
Python
복사
Solver에게 두 노드 사이의 이동 비용(travel cost)을 전달하기 위해서는 SetArcCostEvaluatorOfAllVehicles 함수를 사용하면 됩니다.
이 함수는 모든 차량(Vehicle)의 이동 비용을 콜백 함수에서 반환하는 값과 동일하게 처리합니다.
만약 VRPTW 문제를 해결해야 한다면, 이동 비용으로 거리 행렬(Distance Matrix) 대신 이동 시간 행렬(Travel Time Matrix)을 사용하면 됩니다.
Search 파라미터 설정
search_parameters = pywrapcp.DefaultRoutingSearchParameters()
#Initialization
search_parameters.first_solution_strategy = (routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC)
Python
복사
문제를 해결하기 위해 FirstSolutionStrategy.PATH_CHEAPEST_ARC 방법을 사용하여 초기 해를 생성하고,
그 후 적절한 해답을 찾기 위해 탐색(Search)을 수행합니다.
이 방법은 "시작" 노드에서 출발하여, 가장 저렴한 경로 세그먼트를 형성하는 노드에 연결한 후, 경로를 확장하는 방식으로 작동합니다.
즉, 마지막으로 추가된 노드를 기준으로 가장 비용이 저렴한 다음 노드를 반복적으로 탐색하여 경로를 연장합니다.
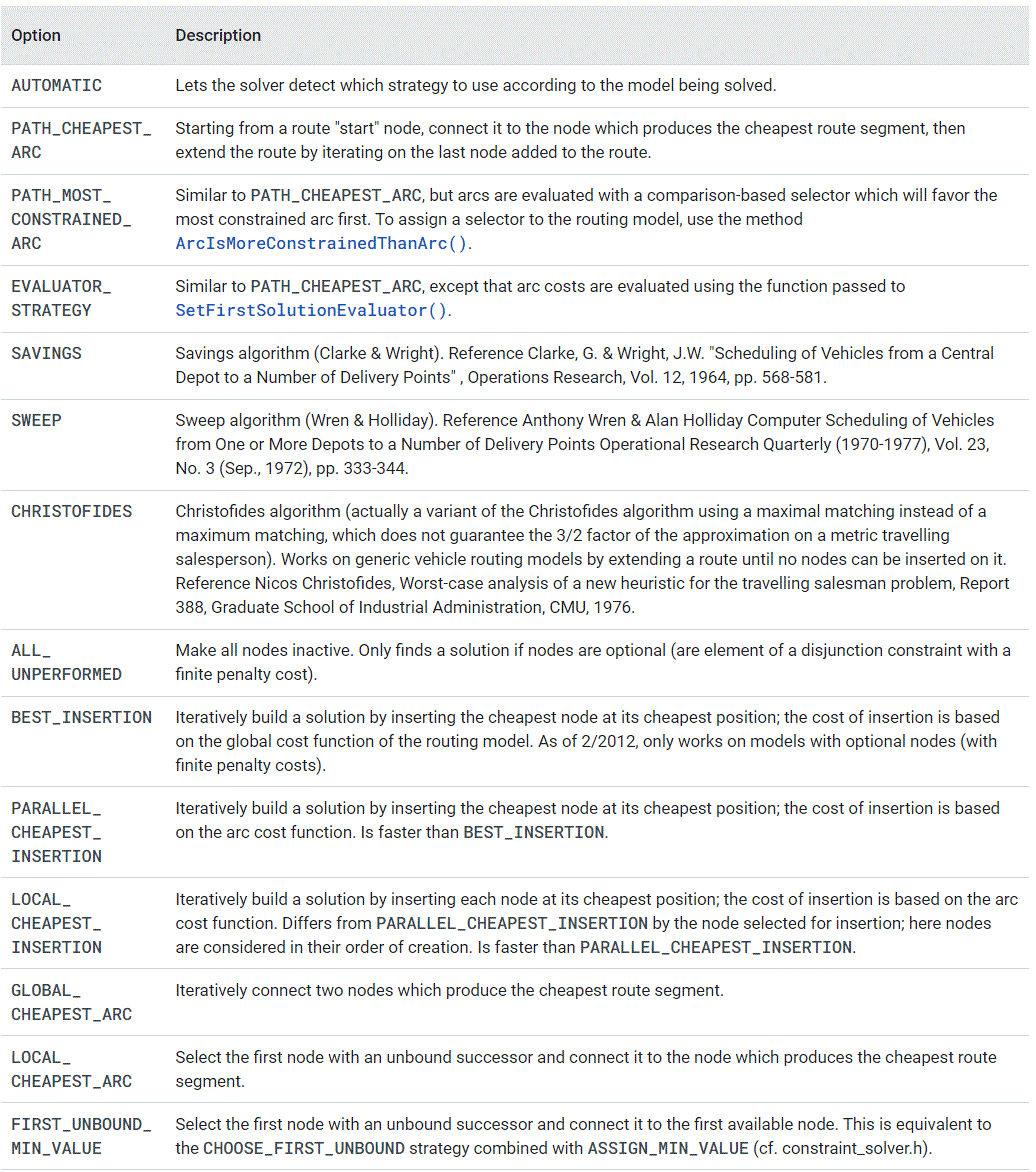
Google OR Tools에서는 초기 해를 생성하기 위한 여러 가지 다른 전략들도 제공합니다.
전체 소스
from ortools.constraint_solver import routing_enums_pb2
from ortools.constraint_solver import pywrapcp
def create_data_model():
"""Stores the data for the problem."""
data = {}
data['distance_matrix'] = [
[0, 22434, 17774, 18808, 15176, 19366, 15279, 8746],
[23022, 0, 5874, 42504, 17816, 14849, 9175, 28979],
[18493, 5874, 0, 39289, 13547, 9880, 4206, 23859],
[18822, 43697, 39049, 0, 41554, 38890, 34055, 19211],
[14876, 16208, 13133, 40235, 0, 20298, 14625, 26710],
[18349, 14787, 9743, 38122, 20759, 0, 6303, 22688],
[15310, 8915, 3871, 34135, 14888, 6593, 0, 21515],
[8761, 30067, 23740, 19122, 27924, 23705, 20552, 0]
]
data['num_vehicles'] = 4
data['depot'] = 0
return data
def print_solution(data, manager, routing, solution):
"""Prints solution on console."""
print(f'Objective: {solution.ObjectiveValue()}')
max_route_distance = 0
for vehicle_id in range(data['num_vehicles']):
index = routing.Start(vehicle_id)
plan_output = 'Route for vehicle {}:\n'.format(vehicle_id)
route_distance = 0
while not routing.IsEnd(index):
plan_output += ' {} -> '.format(manager.IndexToNode(index))
previous_index = index
index = solution.Value(routing.NextVar(index))
route_distance += routing.GetArcCostForVehicle(previous_index, index, vehicle_id)
plan_output += '{}\n'.format(manager.IndexToNode(index))
plan_output += 'Distance of the route: {}m\n'.format(route_distance)
print(plan_output)
max_route_distance = max(route_distance, max_route_distance)
print('Maximum of the route distances: {}m'.format(max_route_distance))
def main():
"""Entry point of the program."""
data = create_data_model()
manager = pywrapcp.RoutingIndexManager(len(data['distance_matrix']), data['num_vehicles'], data['depot'])
routing = pywrapcp.RoutingModel(manager)
def distance_callback(from_index, to_index):
from_node = manager.IndexToNode(from_index)
to_node = manager.IndexToNode(to_index)
return data['distance_matrix'][from_node][to_node]
transit_callback_index = routing.RegisterTransitCallback(distance_callback)
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)
# Add Distance constraint.
dimension_name = 'Distance'
routing.AddDimension(transit_callback_index, 0, 9999999999, True, dimension_name)
distance_dimension = routing.GetDimensionOrDie(dimension_name)
distance_dimension.SetGlobalSpanCostCoefficient(100)
search_parameters = pywrapcp.DefaultRoutingSearchParameters()
#Initialization
search_parameters.first_solution_strategy = (routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC)
solution = routing.SolveWithParameters(search_parameters)
# Print solution on console.
if solution:
print_solution(data, manager, routing, solution)
if __name__ == '__main__':
main()
Python
복사
결과는 아래와 같습니다.
Objective: 4832633
Route for vehicle 0:
0 -> 7 -> 3 -> 0
Distance of the route: 46690m
Route for vehicle 1:
0 -> 6 -> 5 -> 0
Distance of the route: 40221m
Route for vehicle 2:
0 -> 2 -> 1 -> 0
Distance of the route: 46670m
Route for vehicle 3:
0 -> 4 -> 0
Distance of the route: 30052m
Maximum of the route distances: 46690m
Python
복사
Keyword: Logistics Optimization, 물류 최적화, 파이썬, Python, 선형계획법, Linear Programming, Google OR Tools
Reference:
[1] Vehicle Routing Problem by Google, https://developers.google.com/optimization/routing/vrp, Creative Commons Attribution 4.0 License
[2] Capacity Constraints by Google, https://developers.google.com/optimization/routing/cvrp, Creative Commons Attribution 4.0 License