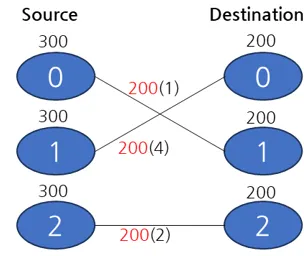
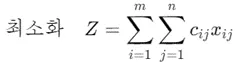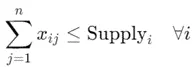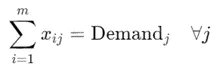Transportation 문제는 공급지에서 수요지로 물품을 운송할 때, 비용을 최소화하는 최적화 문제입니다.
이 문제는 공급처의 재고와 수요처의 필요량을 고려하여, 각 경로에 할당할 물량을 결정하는 방식입니다.
문제의 목표는 전체 운송 비용을 최소화하는 것입니다.
구성
1.
공급지(Supply): 여러 공급지가 있으며, 각 공급지는 특정 수량의 물품을 제공합니다.
2. 수요지(Demand): 여러 수요지가 있으며, 각 수요지는 특정 수량의 물품을 요구합니다.
3. 운송 비용(Cost): 각 공급지에서 각 수요지로 운송하는 데 드는 비용입니다.
기본 가정
1.
공급지에서 공급할 수 있는 물품의 양은 한정되어 있습니다.
2.
수요지에서 요구하는 물품의 양은 정해져 있습니다.
3.
모든 공급지와 수요지의 요구 사항이 충족된다고 가정합니다. 즉, 공급의 총량과 수요의 총량은 일치합니다. (Balanced)
수리적 모델
Transportation 문제는 선형 계획법(Linear Programming)으로 모델링할 수 있습니다.
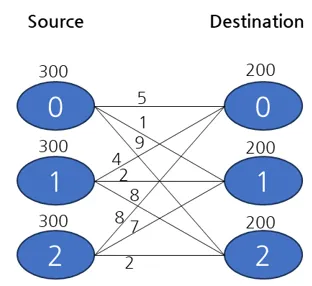
이를 위해 다음과 같은 변수와 제약 조건을 정의합니다. 설명을 위해서 아래와 같은 Transportation 문제가 있다고 가정해 보겠습니다.
목적함수
목적은 운송비용을 최소화 하는 것입니다.
여기에서:
제약식
각 공급지에서 운송되는 물품의 총량은 그 공급지의 최대 공급량을 초과할 수 없습니다.
각 수요지에 배정되는 물품의 총량이 해당 수요지의 요구량과 동일하도록 보장합니다.
이 변경으로 인해 수요량을 정확하게 맞추는 문제가 되며, 공급량이 초과되거나 부족하지 않습니다.
전체 소스
from ortools.linear_solver import pywraplp
def create_data_model():
"""Stores the data for the problem."""
data = {}
# Supply at each source
data['supply'] = [300, 300, 300]
# Demand at each destination
data['demand'] = [200, 200, 200]
# Transportation costs between each source and destination
data['costs'] = [
[5, 1, 9], # Source A to destinations 1, 2, 3
[4, 2, 8], # Source B to destinations 1, 2, 3
[8, 7, 2], # Source C to destinations 1, 2, 3
]
data['num_sources'] = len(data['supply'])
data['num_destinations'] = len(data['demand'])
return data
def main():
# Create the data
data = create_data_model()
# Create the linear solver using the GLOP backend
solver = pywraplp.Solver.CreateSolver('GLOP')
if not solver:
return
# Create variables for each transportation route
x = {}
for i in range(data['num_sources']):
for j in range(data['num_destinations']):
x[(i, j)] = solver.NumVar(0, solver.infinity(), f'x_{i}_{j}')
# Define the objective: Minimize transportation costs
objective = solver.Objective()
for i in range(data['num_sources']):
for j in range(data['num_destinations']):
objective.SetCoefficient(x[(i, j)], data['costs'][i][j])
objective.SetMinimization()
# Constraints: The amount shipped from each source must not exceed supply
for i in range(data['num_sources']):
solver.Add(sum(x[(i, j)] for j in range(data['num_destinations'])) <= data['supply'][i])
# Constraints: The amount shipped to each destination must meet demand
for j in range(data['num_destinations']):
solver.Add(sum(x[(i, j)] for i in range(data['num_sources'])) == data['demand'][j])
# Solve the problem
status = solver.Solve()
# Output the results
if status == pywraplp.Solver.OPTIMAL:
print('Solution:')
print(f'Total transportation cost = {solver.Objective().Value()}\n')
for i in range(data['num_sources']):
for j in range(data['num_destinations']):
print(f'Source {i} to Destination {j}: {x[(i, j)].solution_value()} units')
else:
print('The problem does not have an optimal solution.')
if __name__ == '__main__':
main()
Python
복사
위의 코드를 수행하면 아래와 같은 결과를 얻을 수 있습니다.
Solution:
Total transportation cost = 1400.0
Source 0 to Destination 0: 0.0 units
Source 0 to Destination 1: 200.0 units
Source 0 to Destination 2: 0.0 units
Source 1 to Destination 0: 200.0 units
Source 1 to Destination 1: 0.0 units
Source 1 to Destination 2: 0.0 units
Source 2 to Destination 0: 0.0 units
Source 2 to Destination 1: 0.0 units
Source 2 to Destination 2: 200.0 units
JavaScript
복사
Keyword: Logistics Optimization, 물류 최적화, 파이썬, Python, 선형계획법, Linear Programming, Google OR Tools
Reference: